Eigen::SparseQR< MatrixType_, OrderingType_ > Class Template Reference

Sparse left-looking QR factorization with numerical column pivoting. More...

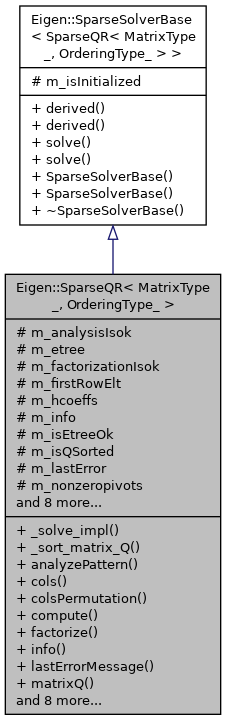
Inheritance diagram for Eigen::SparseQR< MatrixType_, OrderingType_ >:

Public Types
enum	{   ColsAtCompileTime ,   MaxColsAtCompileTime }
typedef Matrix< StorageIndex, Dynamic, 1 >	IndexVector
typedef MatrixType_	MatrixType
typedef OrderingType_	OrderingType
typedef PermutationMatrix< Dynamic, Dynamic, StorageIndex >	PermutationType
typedef SparseMatrix< Scalar, ColMajor, StorageIndex >	QRMatrixType
typedef MatrixType::RealScalar	RealScalar
typedef MatrixType::Scalar	Scalar
typedef Matrix< Scalar, Dynamic, 1 >	ScalarVector
typedef MatrixType::StorageIndex	StorageIndex

Public Member Functions
template<typename Rhs , typename Dest >
bool	_solve_impl (const MatrixBase< Rhs > &B, MatrixBase< Dest > &dest) const
void	_sort_matrix_Q ()
void	analyzePattern (const MatrixType &mat)
	Preprocessing step of a QR factorization. More...
Index	cols () const
const PermutationType &	colsPermutation () const
void	compute (const MatrixType &mat)
void	factorize (const MatrixType &mat)
	Performs the numerical QR factorization of the input matrix. More...
ComputationInfo	info () const
	Reports whether previous computation was successful. More...
std::string	lastErrorMessage () const
SparseQRMatrixQReturnType< SparseQR >	matrixQ () const
const QRMatrixType &	matrixR () const
Index	rank () const
Index	rows () const
void	setPivotThreshold (const RealScalar &threshold)
template<typename Rhs >
const Solve< SparseQR, Rhs >	solve (const MatrixBase< Rhs > &B) const
template<typename Rhs >
const Solve< SparseQR, Rhs >	solve (const SparseMatrixBase< Rhs > &B) const
	SparseQR ()
	SparseQR (const MatrixType &mat)
Public Member Functions inherited from Eigen::SparseSolverBase< SparseQR< MatrixType_, OrderingType_ > >
SparseQR< MatrixType_, OrderingType_ > &	derived ()
const SparseQR< MatrixType_, OrderingType_ > &	derived () const
const Solve< SparseQR< MatrixType_, OrderingType_ >, Rhs >	solve (const MatrixBase< Rhs > &b) const
const Solve< SparseQR< MatrixType_, OrderingType_ >, Rhs >	solve (const SparseMatrixBase< Rhs > &b) const
	SparseSolverBase ()
	SparseSolverBase (SparseSolverBase &&other)
	~SparseSolverBase ()

Protected Types
typedef SparseSolverBase< SparseQR< MatrixType_, OrderingType_ > >	Base

Protected Attributes
bool	m_analysisIsok
IndexVector	m_etree
bool	m_factorizationIsok
IndexVector	m_firstRowElt
ScalarVector	m_hcoeffs
ComputationInfo	m_info
bool	m_isEtreeOk
bool	m_isQSorted
std::string	m_lastError
Index	m_nonzeropivots
PermutationType	m_outputPerm_c
PermutationType	m_perm_c
PermutationType	m_pivotperm
QRMatrixType	m_pmat
QRMatrixType	m_Q
QRMatrixType	m_R
RealScalar	m_threshold
bool	m_useDefaultThreshold
Protected Attributes inherited from Eigen::SparseSolverBase< SparseQR< MatrixType_, OrderingType_ > >
bool	m_isInitialized

Detailed Description

template<typename MatrixType_, typename OrderingType_>
class Eigen::SparseQR< MatrixType_, OrderingType_ >

Sparse left-looking QR factorization with numerical column pivoting.

This class implements a left-looking QR decomposition of sparse matrices with numerical column pivoting. When a column has a norm less than a given tolerance it is implicitly permuted to the end. The QR factorization thus obtained is given by A*P = Q*R where R is upper triangular or trapezoidal.

P is the column permutation which is the product of the fill-reducing and the numerical permutations. Use colsPermutation() to get it.

Q is the orthogonal matrix represented as products of Householder reflectors. Use matrixQ() to get an expression and matrixQ().adjoint() to get the adjoint. You can then apply it to a vector.

R is the sparse triangular or trapezoidal matrix. The later occurs when A is rank-deficient. matrixR().topLeftCorner(rank(), rank()) always returns a triangular factor of full rank.

Template Parameters

MatrixType_	The type of the sparse matrix A, must be a column-major SparseMatrix<>
OrderingType_	The fill-reducing ordering method. See the OrderingMethods module for the list of built-in and external ordering methods.

This class follows the sparse solver concept .

The numerical pivoting strategy and default threshold are the same as in SuiteSparse QR, and detailed in the following paper: Tim Davis, "Algorithm 915, SuiteSparseQR: Multifrontal Multithreaded Rank-Revealing Sparse QR Factorization, ACM Trans. on Math. Soft. 38(1), 2011. Even though it is qualified as "rank-revealing", this strategy might fail for some rank deficient problems. When this class is used to solve linear or least-square problems it is thus strongly recommended to check the accuracy of the computed solution. If it failed, it usually helps to increase the threshold with setPivotThreshold.

Warning

The input sparse matrix A must be in compressed mode (see SparseMatrix::makeCompressed()).

For complex matrices matrixQ().transpose() will actually return the adjoint matrix.

Definition at line 86 of file SparseQR.h.

Member Typedef Documentation

Base

template<typename MatrixType_ , typename OrderingType_ >

typedef SparseSolverBase<SparseQR<MatrixType_,OrderingType_> > Eigen::SparseQR< MatrixType_, OrderingType_ >::Base

protected

Definition at line 89 of file SparseQR.h.

IndexVector

template<typename MatrixType_ , typename OrderingType_ >

typedef Matrix<StorageIndex, Dynamic, 1> Eigen::SparseQR< MatrixType_, OrderingType_ >::IndexVector

Definition at line 99 of file SparseQR.h.

MatrixType

template<typename MatrixType_ , typename OrderingType_ >

typedef MatrixType_ Eigen::SparseQR< MatrixType_, OrderingType_ >::MatrixType

Definition at line 93 of file SparseQR.h.

OrderingType

template<typename MatrixType_ , typename OrderingType_ >

typedef OrderingType_ Eigen::SparseQR< MatrixType_, OrderingType_ >::OrderingType

Definition at line 94 of file SparseQR.h.

PermutationType

template<typename MatrixType_ , typename OrderingType_ >

typedef PermutationMatrix<Dynamic, Dynamic, StorageIndex> Eigen::SparseQR< MatrixType_, OrderingType_ >::PermutationType

Definition at line 101 of file SparseQR.h.

QRMatrixType

template<typename MatrixType_ , typename OrderingType_ >

typedef SparseMatrix<Scalar,ColMajor,StorageIndex> Eigen::SparseQR< MatrixType_, OrderingType_ >::QRMatrixType

Definition at line 98 of file SparseQR.h.

RealScalar

template<typename MatrixType_ , typename OrderingType_ >

typedef MatrixType::RealScalar Eigen::SparseQR< MatrixType_, OrderingType_ >::RealScalar

Definition at line 96 of file SparseQR.h.

Scalar

template<typename MatrixType_ , typename OrderingType_ >

typedef MatrixType::Scalar Eigen::SparseQR< MatrixType_, OrderingType_ >::Scalar

Definition at line 95 of file SparseQR.h.

ScalarVector

template<typename MatrixType_ , typename OrderingType_ >

typedef Matrix<Scalar, Dynamic, 1> Eigen::SparseQR< MatrixType_, OrderingType_ >::ScalarVector

Definition at line 100 of file SparseQR.h.

StorageIndex

template<typename MatrixType_ , typename OrderingType_ >

typedef MatrixType::StorageIndex Eigen::SparseQR< MatrixType_, OrderingType_ >::StorageIndex

Definition at line 97 of file SparseQR.h.

Member Enumeration Documentation

anonymous enum

template<typename MatrixType_ , typename OrderingType_ >

anonymous enum

Enumerator
ColsAtCompileTime
MaxColsAtCompileTime

Definition at line 103 of file SparseQR.h.

         {
      ColsAtCompileTime = MatrixType::ColsAtCompileTime,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

SparseQR() [1/2]

template<typename MatrixType_ , typename OrderingType_ >

Eigen::SparseQR< MatrixType_, OrderingType_ >::SparseQR ( )

inline

Definition at line 109 of file SparseQR.h.

                :  m_analysisIsok(false), m_lastError(""), m_useDefaultThreshold(true),m_isQSorted(false),m_isEtreeOk(false)
    { }

SparseQR() [2/2]

template<typename MatrixType_ , typename OrderingType_ >

Eigen::SparseQR< MatrixType_, OrderingType_ >::SparseQR ( const MatrixType &  mat )

inlineexplicit

Construct a QR factorization of the matrix mat.

Warning

The matrix mat must be in compressed mode (see SparseMatrix::makeCompressed()).

See also

compute()

Definition at line 118 of file SparseQR.h.

                                             : m_analysisIsok(false), m_lastError(""), m_useDefaultThreshold(true),m_isQSorted(false),m_isEtreeOk(false)
    {
      compute(mat);
    }

Member Function Documentation

_solve_impl()

template<typename MatrixType_ , typename OrderingType_ >

template<typename Rhs , typename Dest >

bool Eigen::SparseQR< MatrixType_, OrderingType_ >::_solve_impl ( const MatrixBase< Rhs > &  B, MatrixBase< Dest > &  dest  ) const

inline

Definition at line 207 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
      eigen_assert(this->rows() == B.rows() && "SparseQR::solve() : invalid number of rows in the right hand side matrix");
 
      Index rank = this->rank();
      
      // Compute Q^* * b;
      typename Dest::PlainObject y, b;
      y = this->matrixQ().adjoint() * B;
      b = y;
      
      // Solve with the triangular matrix R
      y.resize((std::max<Index>)(cols(),y.rows()),y.cols());
      y.topRows(rank) = this->matrixR().topLeftCorner(rank, rank).template triangularView<Upper>().solve(b.topRows(rank));
      y.bottomRows(y.rows()-rank).setZero();
      
      // Apply the column permutation
      if (m_perm_c.size())  dest = colsPermutation() * y.topRows(cols());
      else                  dest = y.topRows(cols());
      
      m_info = Success;
      return true;
    }

_sort_matrix_Q()

template<typename MatrixType_ , typename OrderingType_ >

void Eigen::SparseQR< MatrixType_, OrderingType_ >::_sort_matrix_Q ( )

inline

Definition at line 278 of file SparseQR.h.

    {
      if(this->m_isQSorted) return;
      // The matrix Q is sorted during the transposition
      SparseMatrix<Scalar, RowMajor, Index> mQrm(this->m_Q);
      this->m_Q = mQrm;
      this->m_isQSorted = true;
    }

analyzePattern()

template<typename MatrixType , typename OrderingType >

void Eigen::SparseQR< MatrixType, OrderingType >::analyzePattern

(

const MatrixType &

mat

)

Preprocessing step of a QR factorization.

Warning

The matrix mat must be in compressed mode (see SparseMatrix::makeCompressed()).

In this step, the fill-reducing permutation is computed and applied to the columns of A and the column elimination tree is computed as well. Only the sparsity pattern of mat is exploited.

Note

In this step it is assumed that there is no empty row in the matrix mat.

Definition at line 322 of file SparseQR.h.

{
  eigen_assert(mat.isCompressed() && "SparseQR requires a sparse matrix in compressed mode. Call .makeCompressed() before passing it to SparseQR");
  // Copy to a column major matrix if the input is rowmajor
  std::conditional_t<MatrixType::IsRowMajor,QRMatrixType,const MatrixType&> matCpy(mat);
  // Compute the column fill reducing ordering
  OrderingType ord; 
  ord(matCpy, m_perm_c); 
  Index n = mat.cols();
  Index m = mat.rows();
  Index diagSize = (std::min)(m,n);
  
  if (!m_perm_c.size())
  {
    m_perm_c.resize(n);
    m_perm_c.indices().setLinSpaced(n, 0,StorageIndex(n-1));
  }
  
  // Compute the column elimination tree of the permuted matrix
  m_outputPerm_c = m_perm_c.inverse();
  internal::coletree(matCpy, m_etree, m_firstRowElt, m_outputPerm_c.indices().data());
  m_isEtreeOk = true;
  
  m_R.resize(m, n);
  m_Q.resize(m, diagSize);
  
  // Allocate space for nonzero elements: rough estimation
  m_R.reserve(2*mat.nonZeros()); //FIXME Get a more accurate estimation through symbolic factorization with the etree
  m_Q.reserve(2*mat.nonZeros());
  m_hcoeffs.resize(diagSize);
  m_analysisIsok = true;
}

cols()

template<typename MatrixType_ , typename OrderingType_ >

Index Eigen::SparseQR< MatrixType_, OrderingType_ >::cols ( void  ) const

inline

Returns

the number of columns of the represented matrix.

Definition at line 143 of file SparseQR.h.

{ return m_pmat.cols();}

colsPermutation()

template<typename MatrixType_ , typename OrderingType_ >

const PermutationType& Eigen::SparseQR< MatrixType_, OrderingType_ >::colsPermutation ( ) const

inline

Returns

a const reference to the column permutation P that was applied to A such that A*P = Q*R It is the combination of the fill-in reducing permutation and numerical column pivoting.

Definition at line 194 of file SparseQR.h.

    { 
      eigen_assert(m_isInitialized && "Decomposition is not initialized.");
      return m_outputPerm_c;
    }

compute()

template<typename MatrixType_ , typename OrderingType_ >

void Eigen::SparseQR< MatrixType_, OrderingType_ >::compute ( const MatrixType &  mat )

inline

Computes the QR factorization of the sparse matrix mat.

Warning

The matrix mat must be in compressed mode (see SparseMatrix::makeCompressed()).

See also

analyzePattern(), factorize()

Definition at line 129 of file SparseQR.h.

    {
      analyzePattern(mat);
      factorize(mat);
    }

factorize()

template<typename MatrixType , typename OrderingType >

void Eigen::SparseQR< MatrixType, OrderingType >::factorize

(

const MatrixType &

mat

)

Performs the numerical QR factorization of the input matrix.

The function SparseQR::analyzePattern(const MatrixType&) must have been called beforehand with a matrix having the same sparsity pattern than mat.

Parameters

mat	The sparse column-major matrix

Definition at line 363 of file SparseQR.h.

{
  using std::abs;
  
  eigen_assert(m_analysisIsok && "analyzePattern() should be called before this step");
  StorageIndex m = StorageIndex(mat.rows());
  StorageIndex n = StorageIndex(mat.cols());
  StorageIndex diagSize = (std::min)(m,n);
  IndexVector mark((std::max)(m,n)); mark.setConstant(-1);  // Record the visited nodes
  IndexVector Ridx(n), Qidx(m);                             // Store temporarily the row indexes for the current column of R and Q
  Index nzcolR, nzcolQ;                                     // Number of nonzero for the current column of R and Q
  ScalarVector tval(m);                                     // The dense vector used to compute the current column
  RealScalar pivotThreshold = m_threshold;
  
  m_R.setZero();
  m_Q.setZero();
  m_pmat = mat;
  if(!m_isEtreeOk)
  {
    m_outputPerm_c = m_perm_c.inverse();
    internal::coletree(m_pmat, m_etree, m_firstRowElt, m_outputPerm_c.indices().data());
    m_isEtreeOk = true;
  }
 
  m_pmat.uncompress(); // To have the innerNonZeroPtr allocated
  
  // Apply the fill-in reducing permutation lazily:
  {
    // If the input is row major, copy the original column indices,
    // otherwise directly use the input matrix
    // 
    IndexVector originalOuterIndicesCpy;
    const StorageIndex *originalOuterIndices = mat.outerIndexPtr();
    if(MatrixType::IsRowMajor)
    {
      originalOuterIndicesCpy = IndexVector::Map(m_pmat.outerIndexPtr(),n+1);
      originalOuterIndices = originalOuterIndicesCpy.data();
    }
    
    for (int i = 0; i < n; i++)
    {
      Index p = m_perm_c.size() ? m_perm_c.indices()(i) : i;
      m_pmat.outerIndexPtr()[p] = originalOuterIndices[i]; 
      m_pmat.innerNonZeroPtr()[p] = originalOuterIndices[i+1] - originalOuterIndices[i]; 
    }
  }
  
  /* Compute the default threshold as in MatLab, see:
   * Tim Davis, "Algorithm 915, SuiteSparseQR: Multifrontal Multithreaded Rank-Revealing
   * Sparse QR Factorization, ACM Trans. on Math. Soft. 38(1), 2011, Page 8:3 
   */
  if(m_useDefaultThreshold) 
  {
    RealScalar max2Norm = 0.0;
    for (int j = 0; j < n; j++) max2Norm = numext::maxi(max2Norm, m_pmat.col(j).norm());
    if(max2Norm==RealScalar(0))
      max2Norm = RealScalar(1);
    pivotThreshold = 20 * (m + n) * max2Norm * NumTraits<RealScalar>::epsilon();
  }
  
  // Initialize the numerical permutation
  m_pivotperm.setIdentity(n);
  
  StorageIndex nonzeroCol = 0; // Record the number of valid pivots
  m_Q.startVec(0);
 
  // Left looking rank-revealing QR factorization: compute a column of R and Q at a time
  for (StorageIndex col = 0; col < n; ++col)
  {
    mark.setConstant(-1);
    m_R.startVec(col);
    mark(nonzeroCol) = col;
    Qidx(0) = nonzeroCol;
    nzcolR = 0; nzcolQ = 1;
    bool found_diag = nonzeroCol>=m;
    tval.setZero(); 
    
    // Symbolic factorization: find the nonzero locations of the column k of the factors R and Q, i.e.,
    // all the nodes (with indexes lower than rank) reachable through the column elimination tree (etree) rooted at node k.
    // Note: if the diagonal entry does not exist, then its contribution must be explicitly added,
    // thus the trick with found_diag that permits to do one more iteration on the diagonal element if this one has not been found.
    for (typename QRMatrixType::InnerIterator itp(m_pmat, col); itp || !found_diag; ++itp)
    {
      StorageIndex curIdx = nonzeroCol;
      if(itp) curIdx = StorageIndex(itp.row());
      if(curIdx == nonzeroCol) found_diag = true;
      
      // Get the nonzeros indexes of the current column of R
      StorageIndex st = m_firstRowElt(curIdx); // The traversal of the etree starts here
      if (st < 0 )
      {
        m_lastError = "Empty row found during numerical factorization";
        m_info = InvalidInput;
        return;
      }
 
      // Traverse the etree 
      Index bi = nzcolR;
      for (; mark(st) != col; st = m_etree(st))
      {
        Ridx(nzcolR) = st;  // Add this row to the list,
        mark(st) = col;     // and mark this row as visited
        nzcolR++;
      }
 
      // Reverse the list to get the topological ordering
      Index nt = nzcolR-bi;
      for(Index i = 0; i < nt/2; i++) std::swap(Ridx(bi+i), Ridx(nzcolR-i-1));
       
      // Copy the current (curIdx,pcol) value of the input matrix
      if(itp) tval(curIdx) = itp.value();
      else    tval(curIdx) = Scalar(0);
      
      // Compute the pattern of Q(:,k)
      if(curIdx > nonzeroCol && mark(curIdx) != col ) 
      {
        Qidx(nzcolQ) = curIdx;  // Add this row to the pattern of Q,
        mark(curIdx) = col;     // and mark it as visited
        nzcolQ++;
      }
    }
 
    // Browse all the indexes of R(:,col) in reverse order
    for (Index i = nzcolR-1; i >= 0; i--)
    {
      Index curIdx = Ridx(i);
      
      // Apply the curIdx-th householder vector to the current column (temporarily stored into tval)
      Scalar tdot(0);
      
      // First compute q' * tval
      tdot = m_Q.col(curIdx).dot(tval);
 
      tdot *= m_hcoeffs(curIdx);
      
      // Then update tval = tval - q * tau
      // FIXME: tval -= tdot * m_Q.col(curIdx) should amount to the same (need to check/add support for efficient "dense ?= sparse")
      for (typename QRMatrixType::InnerIterator itq(m_Q, curIdx); itq; ++itq)
        tval(itq.row()) -= itq.value() * tdot;
 
      // Detect fill-in for the current column of Q
      if(m_etree(Ridx(i)) == nonzeroCol)
      {
        for (typename QRMatrixType::InnerIterator itq(m_Q, curIdx); itq; ++itq)
        {
          StorageIndex iQ = StorageIndex(itq.row());
          if (mark(iQ) != col)
          {
            Qidx(nzcolQ++) = iQ;  // Add this row to the pattern of Q,
            mark(iQ) = col;       // and mark it as visited
          }
        }
      }
    } // End update current column
    
    Scalar tau = RealScalar(0);
    RealScalar beta = 0;
    
    if(nonzeroCol < diagSize)
    {
      // Compute the Householder reflection that eliminate the current column
      // FIXME this step should call the Householder module.
      Scalar c0 = nzcolQ ? tval(Qidx(0)) : Scalar(0);
      
      // First, the squared norm of Q((col+1):m, col)
      RealScalar sqrNorm = 0.;
      for (Index itq = 1; itq < nzcolQ; ++itq) sqrNorm += numext::abs2(tval(Qidx(itq)));
      if(sqrNorm == RealScalar(0) && numext::imag(c0) == RealScalar(0))
      {
        beta = numext::real(c0);
        tval(Qidx(0)) = 1;
      }
      else
      {
        using std::sqrt;
        beta = sqrt(numext::abs2(c0) + sqrNorm);
        if(numext::real(c0) >= RealScalar(0))
          beta = -beta;
        tval(Qidx(0)) = 1;
        for (Index itq = 1; itq < nzcolQ; ++itq)
          tval(Qidx(itq)) /= (c0 - beta);
        tau = numext::conj((beta-c0) / beta);
          
      }
    }
 
    // Insert values in R
    for (Index  i = nzcolR-1; i >= 0; i--)
    {
      Index curIdx = Ridx(i);
      if(curIdx < nonzeroCol) 
      {
        m_R.insertBackByOuterInnerUnordered(col, curIdx) = tval(curIdx);
        tval(curIdx) = Scalar(0.);
      }
    }
 
    if(nonzeroCol < diagSize && abs(beta) >= pivotThreshold)
    {
      m_R.insertBackByOuterInner(col, nonzeroCol) = beta;
      // The householder coefficient
      m_hcoeffs(nonzeroCol) = tau;
      // Record the householder reflections
      for (Index itq = 0; itq < nzcolQ; ++itq)
      {
        Index iQ = Qidx(itq);
        m_Q.insertBackByOuterInnerUnordered(nonzeroCol,iQ) = tval(iQ);
        tval(iQ) = Scalar(0.);
      }
      nonzeroCol++;
      if(nonzeroCol<diagSize)
        m_Q.startVec(nonzeroCol);
    }
    else
    {
      // Zero pivot found: move implicitly this column to the end
      for (Index j = nonzeroCol; j < n-1; j++) 
        std::swap(m_pivotperm.indices()(j), m_pivotperm.indices()[j+1]);
      
      // Recompute the column elimination tree
      internal::coletree(m_pmat, m_etree, m_firstRowElt, m_pivotperm.indices().data());
      m_isEtreeOk = false;
    }
  }
  
  m_hcoeffs.tail(diagSize-nonzeroCol).setZero();
  
  // Finalize the column pointers of the sparse matrices R and Q
  m_Q.finalize();
  m_Q.makeCompressed();
  m_R.finalize();
  m_R.makeCompressed();
  m_isQSorted = false;
 
  m_nonzeropivots = nonzeroCol;
  
  if(nonzeroCol<n)
  {
    // Permute the triangular factor to put the 'dead' columns to the end
    QRMatrixType tempR(m_R);
    m_R = tempR * m_pivotperm;
    
    // Update the column permutation
    m_outputPerm_c = m_outputPerm_c * m_pivotperm;
  }
  
  m_isInitialized = true; 
  m_factorizationIsok = true;
  m_info = Success;
}

info()

template<typename MatrixType_ , typename OrderingType_ >

ComputationInfo Eigen::SparseQR< MatrixType_, OrderingType_ >::info ( ) const

inline

Reports whether previous computation was successful.

Returns

Success if computation was successful, NumericalIssue if the QR factorization reports a numerical problem InvalidInput if the input matrix is invalid

See also

iparm()

Definition at line 270 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "Decomposition is not initialized.");
      return m_info;
    }

lastErrorMessage()

template<typename MatrixType_ , typename OrderingType_ >

std::string Eigen::SparseQR< MatrixType_, OrderingType_ >::lastErrorMessage ( ) const

inline

Returns

A string describing the type of error. This method is provided to ease debugging, not to handle errors.

Definition at line 203 of file SparseQR.h.

{ return m_lastError; }

matrixQ()

template<typename MatrixType_ , typename OrderingType_ >

SparseQRMatrixQReturnType<SparseQR> Eigen::SparseQR< MatrixType_, OrderingType_ >::matrixQ ( void  ) const

inline

Returns

an expression of the matrix Q as products of sparse Householder reflectors. The common usage of this function is to apply it to a dense matrix or vector

VectorXd B1, B2;
// Initialize B1
B2 = matrixQ() * B1;

To get a plain SparseMatrix representation of Q:

SparseMatrix<double> Q;
Q = SparseQR<SparseMatrix<double> >(A).matrixQ();

Internally, this call simply performs a sparse product between the matrix Q and a sparse identity matrix. However, due to the fact that the sparse reflectors are stored unsorted, two transpositions are needed to sort them before performing the product.

Definition at line 188 of file SparseQR.h.

    { return SparseQRMatrixQReturnType<SparseQR>(*this); }

matrixR()

template<typename MatrixType_ , typename OrderingType_ >

const QRMatrixType& Eigen::SparseQR< MatrixType_, OrderingType_ >::matrixR ( ) const

inline

Returns

a const reference to the sparse upper triangular matrix R of the QR factorization.

Warning

The entries of the returned matrix are not sorted. This means that using it in algorithms expecting sorted entries will fail. This include random coefficient accesses (SpaseMatrix::coeff()), and coefficient-wise operations. Matrix products and triangular solves are fine though.

To sort the entries, you can assign it to a row-major matrix, and if a column-major matrix is required, you can copy it again:

SparseMatrix<double>          R  = qr.matrixR();  // column-major, not sorted!
SparseMatrix<double,RowMajor> Rr = qr.matrixR();  // row-major, sorted
SparseMatrix<double>          Rc = Rr;            // column-major, sorted

Definition at line 158 of file SparseQR.h.

{ return m_R; }

rank()

template<typename MatrixType_ , typename OrderingType_ >

Index Eigen::SparseQR< MatrixType_, OrderingType_ >::rank ( ) const

inline

Returns

the number of non linearly dependent columns as determined by the pivoting threshold.

See also

setPivotThreshold()

Definition at line 164 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
      return m_nonzeropivots; 
    }

rows()

template<typename MatrixType_ , typename OrderingType_ >

Index Eigen::SparseQR< MatrixType_, OrderingType_ >::rows ( void  ) const

inline

Returns

the number of rows of the represented matrix.

Definition at line 139 of file SparseQR.h.

{ return m_pmat.rows(); }

setPivotThreshold()

template<typename MatrixType_ , typename OrderingType_ >

void Eigen::SparseQR< MatrixType_, OrderingType_ >::setPivotThreshold ( const RealScalar &  threshold )

inline

Sets the threshold that is used to determine linearly dependent columns during the factorization.

In practice, if during the factorization the norm of the column that has to be eliminated is below this threshold, then the entire column is treated as zero, and it is moved at the end.

Definition at line 237 of file SparseQR.h.

    {
      m_useDefaultThreshold = false;
      m_threshold = threshold;
    }

solve() [1/2]

template<typename MatrixType_ , typename OrderingType_ >

template<typename Rhs >

const Solve<SparseQR, Rhs> Eigen::SparseQR< MatrixType_, OrderingType_ >::solve ( const MatrixBase< Rhs > &  B ) const

inline

Returns

the solution X of \( A X = B \) using the current decomposition of A.

See also

compute()

Definition at line 248 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
      eigen_assert(this->rows() == B.rows() && "SparseQR::solve() : invalid number of rows in the right hand side matrix");
      return Solve<SparseQR, Rhs>(*this, B.derived());
    }

solve() [2/2]

template<typename MatrixType_ , typename OrderingType_ >

template<typename Rhs >

const Solve<SparseQR, Rhs> Eigen::SparseQR< MatrixType_, OrderingType_ >::solve ( const SparseMatrixBase< Rhs > &  B ) const

inline

Definition at line 255 of file SparseQR.h.

    {
          eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
          eigen_assert(this->rows() == B.rows() && "SparseQR::solve() : invalid number of rows in the right hand side matrix");
          return Solve<SparseQR, Rhs>(*this, B.derived());
    }

Member Data Documentation

m_analysisIsok

template<typename MatrixType_ , typename OrderingType_ >

bool Eigen::SparseQR< MatrixType_, OrderingType_ >::m_analysisIsok

protected

Definition at line 289 of file SparseQR.h.

m_etree

template<typename MatrixType_ , typename OrderingType_ >

IndexVector Eigen::SparseQR< MatrixType_, OrderingType_ >::m_etree

protected

Definition at line 303 of file SparseQR.h.

m_factorizationIsok

template<typename MatrixType_ , typename OrderingType_ >

bool Eigen::SparseQR< MatrixType_, OrderingType_ >::m_factorizationIsok

protected

Definition at line 290 of file SparseQR.h.

m_firstRowElt

template<typename MatrixType_ , typename OrderingType_ >

IndexVector Eigen::SparseQR< MatrixType_, OrderingType_ >::m_firstRowElt

protected

Definition at line 304 of file SparseQR.h.

m_hcoeffs

template<typename MatrixType_ , typename OrderingType_ >

ScalarVector Eigen::SparseQR< MatrixType_, OrderingType_ >::m_hcoeffs

protected

Definition at line 296 of file SparseQR.h.

m_info

template<typename MatrixType_ , typename OrderingType_ >

ComputationInfo Eigen::SparseQR< MatrixType_, OrderingType_ >::m_info

mutableprotected

Definition at line 291 of file SparseQR.h.

m_isEtreeOk

template<typename MatrixType_ , typename OrderingType_ >

bool Eigen::SparseQR< MatrixType_, OrderingType_ >::m_isEtreeOk

protected

Definition at line 306 of file SparseQR.h.

m_isQSorted

template<typename MatrixType_ , typename OrderingType_ >

bool Eigen::SparseQR< MatrixType_, OrderingType_ >::m_isQSorted

protected

Definition at line 305 of file SparseQR.h.

m_lastError

template<typename MatrixType_ , typename OrderingType_ >

std::string Eigen::SparseQR< MatrixType_, OrderingType_ >::m_lastError

protected

Definition at line 292 of file SparseQR.h.

m_nonzeropivots

template<typename MatrixType_ , typename OrderingType_ >

Index Eigen::SparseQR< MatrixType_, OrderingType_ >::m_nonzeropivots

protected

Definition at line 302 of file SparseQR.h.

m_outputPerm_c

template<typename MatrixType_ , typename OrderingType_ >

PermutationType Eigen::SparseQR< MatrixType_, OrderingType_ >::m_outputPerm_c

protected

Definition at line 299 of file SparseQR.h.

m_perm_c

template<typename MatrixType_ , typename OrderingType_ >

PermutationType Eigen::SparseQR< MatrixType_, OrderingType_ >::m_perm_c

protected

Definition at line 297 of file SparseQR.h.

m_pivotperm

template<typename MatrixType_ , typename OrderingType_ >

PermutationType Eigen::SparseQR< MatrixType_, OrderingType_ >::m_pivotperm

protected

Definition at line 298 of file SparseQR.h.

m_pmat

template<typename MatrixType_ , typename OrderingType_ >

QRMatrixType Eigen::SparseQR< MatrixType_, OrderingType_ >::m_pmat

protected

Definition at line 293 of file SparseQR.h.

m_Q

template<typename MatrixType_ , typename OrderingType_ >

QRMatrixType Eigen::SparseQR< MatrixType_, OrderingType_ >::m_Q

protected

Definition at line 295 of file SparseQR.h.

m_R

template<typename MatrixType_ , typename OrderingType_ >

QRMatrixType Eigen::SparseQR< MatrixType_, OrderingType_ >::m_R

protected

Definition at line 294 of file SparseQR.h.

m_threshold

template<typename MatrixType_ , typename OrderingType_ >

RealScalar Eigen::SparseQR< MatrixType_, OrderingType_ >::m_threshold

protected

Definition at line 300 of file SparseQR.h.

m_useDefaultThreshold

template<typename MatrixType_ , typename OrderingType_ >

bool Eigen::SparseQR< MatrixType_, OrderingType_ >::m_useDefaultThreshold

protected

Definition at line 301 of file SparseQR.h.

---

The documentation for this class was generated from the following file:

• SparseQR.h