|
| enum | {
MaxRowsAtCompileTime
,
MaxColsAtCompileTime
,
UpLo
} |
| |
| typedef SolverBase< LDLT > | Base |
| |
| typedef MatrixType_ | MatrixType |
| |
| typedef PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime > | PermutationType |
| |
| typedef Matrix< Scalar, RowsAtCompileTime, 1, 0, MaxRowsAtCompileTime, 1 > | TmpMatrixType |
| |
| typedef internal::LDLT_Traits< MatrixType, UpLo > | Traits |
| |
| typedef Transpositions< RowsAtCompileTime, MaxRowsAtCompileTime > | TranspositionType |
| |
| enum | |
| |
| typedef std::conditional_t< NumTraits< Scalar >::IsComplex, CwiseUnaryOp< internal::scalar_conjugate_op< Scalar >, const ConstTransposeReturnType >, const ConstTransposeReturnType > | AdjointReturnType |
| |
| typedef EigenBase< LDLT< MatrixType_, UpLo_ > > | Base |
| |
| typedef Scalar | CoeffReturnType |
| |
| typedef Transpose< const LDLT< MatrixType_, UpLo_ > > | ConstTransposeReturnType |
| |
| typedef internal::traits< LDLT< MatrixType_, UpLo_ > >::Scalar | Scalar |
| |
| typedef Eigen::Index | Index |
| | The interface type of indices. More...
|
| |
| typedef internal::traits< Derived >::StorageKind | StorageKind |
| |
|
| const LDLT & | adjoint () const |
| |
| EIGEN_CONSTEXPR Index | cols () const EIGEN_NOEXCEPT |
| |
| template<typename InputType > |
| LDLT< MatrixType, UpLo_ > & | compute (const EigenBase< InputType > &a) |
| |
| template<typename InputType > |
| LDLT & | compute (const EigenBase< InputType > &matrix) |
| |
| ComputationInfo | info () const |
| | Reports whether previous computation was successful. More...
|
| |
| bool | isNegative (void) const |
| |
| bool | isPositive () const |
| |
| | LDLT () |
| | Default Constructor. More...
|
| |
| template<typename InputType > |
| | LDLT (const EigenBase< InputType > &matrix) |
| | Constructor with decomposition. More...
|
| |
| template<typename InputType > |
| | LDLT (EigenBase< InputType > &matrix) |
| | Constructs a LDLT factorization from a given matrix. More...
|
| |
| | LDLT (Index size) |
| | Default Constructor with memory preallocation. More...
|
| |
| Traits::MatrixL | matrixL () const |
| |
| const MatrixType & | matrixLDLT () const |
| |
| Traits::MatrixU | matrixU () const |
| |
| template<typename Derived > |
| LDLT & | rankUpdate (const MatrixBase< Derived > &w, const RealScalar &alpha=1) |
| |
| template<typename Derived > |
| LDLT< MatrixType, UpLo_ > & | rankUpdate (const MatrixBase< Derived > &w, const typename LDLT< MatrixType, UpLo_ >::RealScalar &sigma) |
| |
| RealScalar | rcond () const |
| |
| MatrixType | reconstructedMatrix () const |
| |
| EIGEN_CONSTEXPR Index | rows () const EIGEN_NOEXCEPT |
| |
| void | setZero () |
| |
| template<typename Rhs > |
| const Solve< LDLT, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| |
| template<typename Derived > |
| bool | solveInPlace (MatrixBase< Derived > &bAndX) const |
| |
| const TranspositionType & | transpositionsP () const |
| |
| Diagonal< const MatrixType > | vectorD () const |
| |
| const AdjointReturnType | adjoint () const |
| |
| LDLT< MatrixType_, UpLo_ > & | derived () |
| |
| const LDLT< MatrixType_, UpLo_ > & | derived () const |
| |
| const Solve< LDLT< MatrixType_, UpLo_ >, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| |
| | SolverBase () |
| |
| const ConstTransposeReturnType | transpose () const |
| |
| | ~SolverBase () |
| |
| template<typename Dest > |
| void | addTo (Dest &dst) const |
| |
| template<typename Dest > |
| void | applyThisOnTheLeft (Dest &dst) const |
| |
| template<typename Dest > |
| void | applyThisOnTheRight (Dest &dst) const |
| |
| EIGEN_CONSTEXPR Index | cols () const EIGEN_NOEXCEPT |
| |
| Derived & | const_cast_derived () const |
| |
| const Derived & | const_derived () const |
| |
| Derived & | derived () |
| |
| const Derived & | derived () const |
| |
| template<typename Dest > |
| void | evalTo (Dest &dst) const |
| |
| EIGEN_CONSTEXPR Index | rows () const EIGEN_NOEXCEPT |
| |
| EIGEN_CONSTEXPR Index | size () const EIGEN_NOEXCEPT |
| |
| template<typename Dest > |
| void | subTo (Dest &dst) const |
| |
template<typename MatrixType_, int UpLo_>
class Eigen::LDLT< MatrixType_, UpLo_ >
Robust Cholesky decomposition of a matrix with pivoting.
- Template Parameters
-
| MatrixType_ | the type of the matrix of which to compute the LDL^T Cholesky decomposition |
| UpLo_ | the triangular part that will be used for the decomposition: Lower (default) or Upper. The other triangular part won't be read. |
Perform a robust Cholesky decomposition of a positive semidefinite or negative semidefinite matrix \( A \) such that \( A = P^TLDL^*P \), where P is a permutation matrix, L is lower triangular with a unit diagonal and D is a diagonal matrix.
The decomposition uses pivoting to ensure stability, so that D will have zeros in the bottom right rank(A) - n submatrix. Avoiding the square root on D also stabilizes the computation.
Remember that Cholesky decompositions are not rank-revealing. Also, do not use a Cholesky decomposition to determine whether a system of equations has a solution.
This class supports the inplace decomposition mechanism.
- See also
- MatrixBase::ldlt(), SelfAdjointView::ldlt(), class LLT
Definition at line 61 of file LDLT.h.
template<typename MatrixType_ , int UpLo_>
template<typename Rhs >
- Returns
- a solution x of \( A x = b \) using the current decomposition of A.
This function also supports in-place solves using the syntax x = decompositionObject.solve(x) .
This method just tries to find as good a solution as possible. If you want to check whether a solution exists or if it is accurate, just call this function to get a result and then compute the error of this result, or use MatrixBase::isApprox() directly, for instance like this:
bool a_solution_exists = (
A*result).
isApprox(
b, precision);
bool isApprox(const Scalar &x, const Scalar &y, const typename NumTraits< Scalar >::Real &precision=NumTraits< Scalar >::dummy_precision())
This method avoids dividing by zero, so that the non-existence of a solution doesn't by itself mean that you'll get inf or nan values.
More precisely, this method solves \( A x = b \) using the decomposition \( A = P^T L D L^* P \) by solving the systems \( P^T y_1 = b \), \( L y_2 = y_1 \), \( D y_3 = y_2 \), \( L^* y_4 = y_3 \) and \( P x = y_4 \) in succession. If the matrix \( A \) is singular, then \( D \) will also be singular (all the other matrices are invertible). In that case, the least-square solution of \( D y_3 = y_2 \) is computed. This does not mean that this function computes the least-square solution of \( A x = b \) if \( A \) is singular.
- See also
- MatrixBase::ldlt(), SelfAdjointView::ldlt()
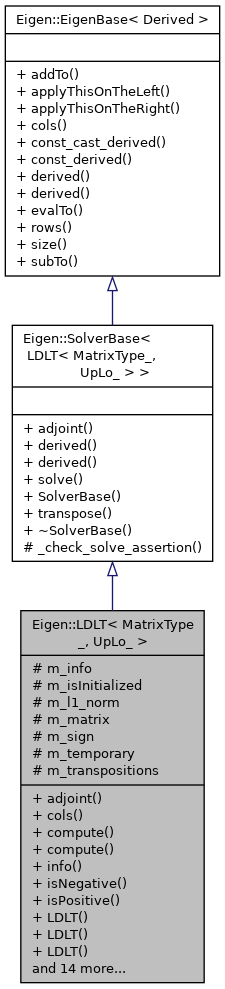
 Inheritance diagram for Eigen::LDLT< MatrixType_, UpLo_ >:
Inheritance diagram for Eigen::LDLT< MatrixType_, UpLo_ >: Public Member Functions inherited from Eigen::SolverBase< LDLT< MatrixType_, UpLo_ > >
Public Member Functions inherited from Eigen::SolverBase< LDLT< MatrixType_, UpLo_ > > Public Member Functions inherited from Eigen::EigenBase< Derived >
Public Member Functions inherited from Eigen::EigenBase< Derived > Protected Member Functions inherited from Eigen::SolverBase< LDLT< MatrixType_, UpLo_ > >
Protected Member Functions inherited from Eigen::SolverBase< LDLT< MatrixType_, UpLo_ > >