Eigen::IncompleteLUT< Scalar_, StorageIndex_ > Class Template Reference

Incomplete LU factorization with dual-threshold strategy. More...

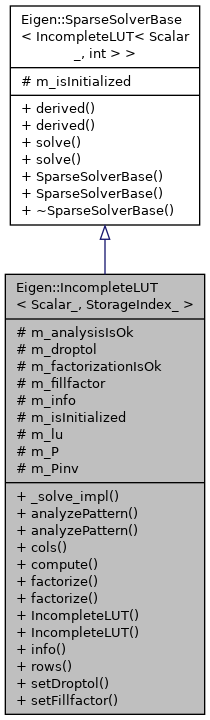
Inheritance diagram for Eigen::IncompleteLUT< Scalar_, StorageIndex_ >:

Classes
struct	keep_diag

Public Types
enum	{   ColsAtCompileTime ,   MaxColsAtCompileTime }
typedef SparseMatrix< Scalar, RowMajor, StorageIndex >	FactorType
typedef NumTraits< Scalar >::Real	RealScalar
typedef Scalar_	Scalar
typedef StorageIndex_	StorageIndex
typedef Matrix< Scalar, Dynamic, 1 >	Vector
typedef Matrix< StorageIndex, Dynamic, 1 >	VectorI

Public Member Functions
template<typename Rhs , typename Dest >
void	_solve_impl (const Rhs &b, Dest &x) const
template<typename MatrixType >
void	analyzePattern (const MatrixType &amat)
template<typename MatrixType_ >
void	analyzePattern (const MatrixType_ &amat)
EIGEN_CONSTEXPR Index	cols () const EIGEN_NOEXCEPT
template<typename MatrixType >
IncompleteLUT &	compute (const MatrixType &amat)
template<typename MatrixType >
void	factorize (const MatrixType &amat)
template<typename MatrixType_ >
void	factorize (const MatrixType_ &amat)
	IncompleteLUT ()
template<typename MatrixType >
	IncompleteLUT (const MatrixType &mat, const RealScalar &droptol=NumTraits< Scalar >::dummy_precision(), int fillfactor=10)
ComputationInfo	info () const
	Reports whether previous computation was successful. More...
EIGEN_CONSTEXPR Index	rows () const EIGEN_NOEXCEPT
void	setDroptol (const RealScalar &droptol)
void	setFillfactor (int fillfactor)
Public Member Functions inherited from Eigen::SparseSolverBase< IncompleteLUT< Scalar_, int > >
IncompleteLUT< Scalar_, int > &	derived ()
const IncompleteLUT< Scalar_, int > &	derived () const
const Solve< IncompleteLUT< Scalar_, int >, Rhs >	solve (const MatrixBase< Rhs > &b) const
const Solve< IncompleteLUT< Scalar_, int >, Rhs >	solve (const SparseMatrixBase< Rhs > &b) const
	SparseSolverBase ()
	SparseSolverBase (SparseSolverBase &&other)
	~SparseSolverBase ()

Protected Types
typedef SparseSolverBase< IncompleteLUT >	Base

Protected Attributes
bool	m_analysisIsOk
RealScalar	m_droptol
bool	m_factorizationIsOk
int	m_fillfactor
ComputationInfo	m_info
bool	m_isInitialized
FactorType	m_lu
PermutationMatrix< Dynamic, Dynamic, StorageIndex >	m_P
PermutationMatrix< Dynamic, Dynamic, StorageIndex >	m_Pinv
Protected Attributes inherited from Eigen::SparseSolverBase< IncompleteLUT< Scalar_, int > >
bool	m_isInitialized

Detailed Description

template<typename Scalar_, typename StorageIndex_ = int>
class Eigen::IncompleteLUT< Scalar_, StorageIndex_ >

Incomplete LU factorization with dual-threshold strategy.

This class follows the sparse solver concept .

During the numerical factorization, two dropping rules are used : 1) any element whose magnitude is less than some tolerance is dropped. This tolerance is obtained by multiplying the input tolerance droptol by the average magnitude of all the original elements in the current row. 2) After the elimination of the row, only the fill largest elements in the L part and the fill largest elements in the U part are kept (in addition to the diagonal element ). Note that fill is computed from the input parameter fillfactor which is used the ratio to control the fill_in relatively to the initial number of nonzero elements.

The two extreme cases are when droptol=0 (to keep all the fill*2 largest elements) and when fill=n/2 with droptol being different to zero.

References : Yousef Saad, ILUT: A dual threshold incomplete LU factorization, Numerical Linear Algebra with Applications, 1(4), pp 387-402, 1994.

NOTE : The following implementation is derived from the ILUT implementation in the SPARSKIT package, Copyright (C) 2005, the Regents of the University of Minnesota released under the terms of the GNU LGPL: http://www-users.cs.umn.edu/~saad/software/SPARSKIT/README However, Yousef Saad gave us permission to relicense his ILUT code to MPL2. See the Eigen mailing list archive, thread: ILUT, date: July 8, 2012: http://listengine.tuxfamily.org/lists.tuxfamily.org/eigen/2012/07/msg00064.html alternatively, on GMANE: http://comments.gmane.org/gmane.comp.lib.eigen/3302

Definition at line 101 of file IncompleteLUT.h.

Member Typedef Documentation

Base

template<typename Scalar_ , typename StorageIndex_ = int>

typedef SparseSolverBase<IncompleteLUT> Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::Base

protected

Definition at line 104 of file IncompleteLUT.h.

FactorType

template<typename Scalar_ , typename StorageIndex_ = int>

typedef SparseMatrix<Scalar,RowMajor,StorageIndex> Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::FactorType

Definition at line 112 of file IncompleteLUT.h.

RealScalar

template<typename Scalar_ , typename StorageIndex_ = int>

typedef NumTraits<Scalar>::Real Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::RealScalar

Definition at line 109 of file IncompleteLUT.h.

Scalar

template<typename Scalar_ , typename StorageIndex_ = int>

typedef Scalar_ Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::Scalar

Definition at line 107 of file IncompleteLUT.h.

StorageIndex

template<typename Scalar_ , typename StorageIndex_ = int>

typedef StorageIndex_ Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::StorageIndex

Definition at line 108 of file IncompleteLUT.h.

Vector

template<typename Scalar_ , typename StorageIndex_ = int>

typedef Matrix<Scalar,Dynamic,1> Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::Vector

Definition at line 110 of file IncompleteLUT.h.

VectorI

template<typename Scalar_ , typename StorageIndex_ = int>

typedef Matrix<StorageIndex,Dynamic,1> Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::VectorI

Definition at line 111 of file IncompleteLUT.h.

Member Enumeration Documentation

anonymous enum

template<typename Scalar_ , typename StorageIndex_ = int>

anonymous enum

Enumerator
ColsAtCompileTime
MaxColsAtCompileTime

Definition at line 114 of file IncompleteLUT.h.

         {
      ColsAtCompileTime = Dynamic,
      MaxColsAtCompileTime = Dynamic
    };

Constructor & Destructor Documentation

IncompleteLUT() [1/2]

template<typename Scalar_ , typename StorageIndex_ = int>

Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::IncompleteLUT ( )

inline

Definition at line 121 of file IncompleteLUT.h.

      : m_droptol(NumTraits<Scalar>::dummy_precision()), m_fillfactor(10),
        m_analysisIsOk(false), m_factorizationIsOk(false)
    {}

IncompleteLUT() [2/2]

template<typename Scalar_ , typename StorageIndex_ = int>

template<typename MatrixType >

Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::IncompleteLUT ( const MatrixType &  mat, const RealScalar &  droptol = NumTraits<Scalar>::dummy_precision(), int  fillfactor = 10  )

inlineexplicit

Definition at line 127 of file IncompleteLUT.h.

      : m_droptol(droptol),m_fillfactor(fillfactor),
        m_analysisIsOk(false),m_factorizationIsOk(false)
    {
      eigen_assert(fillfactor != 0);
      compute(mat);
    }

Member Function Documentation

_solve_impl()

template<typename Scalar_ , typename StorageIndex_ = int>

template<typename Rhs , typename Dest >

void Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::_solve_impl ( const Rhs &  b, Dest &  x  ) const

inline

Definition at line 173 of file IncompleteLUT.h.

    {
      x = m_Pinv * b;
      x = m_lu.template triangularView<UnitLower>().solve(x);
      x = m_lu.template triangularView<Upper>().solve(x);
      x = m_P * x;
    }

analyzePattern() [1/2]

template<typename Scalar_ , typename StorageIndex_ = int>

template<typename MatrixType >

void Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::analyzePattern

(

const MatrixType &

amat

)

analyzePattern() [2/2]

template<typename Scalar_ , typename StorageIndex_ = int>

template<typename MatrixType_ >

void Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::analyzePattern

(

const MatrixType_ &

amat

)

Definition at line 225 of file IncompleteLUT.h.

{
  // Compute the Fill-reducing permutation
  // Since ILUT does not perform any numerical pivoting,
  // it is highly preferable to keep the diagonal through symmetric permutations.
  // To this end, let's symmetrize the pattern and perform AMD on it.
  SparseMatrix<Scalar,ColMajor, StorageIndex> mat1 = amat;
  SparseMatrix<Scalar,ColMajor, StorageIndex> mat2 = amat.transpose();
  // FIXME for a matrix with nearly symmetric pattern, mat2+mat1 is the appropriate choice.
  //       on the other hand for a really non-symmetric pattern, mat2*mat1 should be preferred...
  SparseMatrix<Scalar,ColMajor, StorageIndex> AtA = mat2 + mat1;
  AMDOrdering<StorageIndex> ordering;
  ordering(AtA,m_P);
  m_Pinv  = m_P.inverse(); // cache the inverse permutation
  m_analysisIsOk = true;
  m_factorizationIsOk = false;
  m_isInitialized = true;
}

cols()

template<typename Scalar_ , typename StorageIndex_ = int>

EIGEN_CONSTEXPR Index Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::cols ( void  ) const

inline

Definition at line 137 of file IncompleteLUT.h.

{ return m_lu.cols(); }

compute()

template<typename Scalar_ , typename StorageIndex_ = int>

template<typename MatrixType >

IncompleteLUT& Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::compute ( const MatrixType &  amat )

inline

Compute an incomplete LU factorization with dual threshold on the matrix mat No pivoting is done in this version

Definition at line 162 of file IncompleteLUT.h.

    {
      analyzePattern(amat);
      factorize(amat);
      return *this;
    }

factorize() [1/2]

template<typename Scalar_ , typename StorageIndex_ = int>

template<typename MatrixType >

void Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::factorize

(

const MatrixType &

amat

)

factorize() [2/2]

template<typename Scalar_ , typename StorageIndex_ = int>

template<typename MatrixType_ >

void Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::factorize

(

const MatrixType_ &

amat

)

Definition at line 246 of file IncompleteLUT.h.

{
  using std::sqrt;
  using std::swap;
  using std::abs;
  using internal::convert_index;
 
  eigen_assert((amat.rows() == amat.cols()) && "The factorization should be done on a square matrix");
  Index n = amat.cols();  // Size of the matrix
  m_lu.resize(n,n);
  // Declare Working vectors and variables
  Vector u(n) ;     // real values of the row -- maximum size is n --
  VectorI ju(n);   // column position of the values in u -- maximum size  is n
  VectorI jr(n);   // Indicate the position of the nonzero elements in the vector u -- A zero location is indicated by -1
 
  // Apply the fill-reducing permutation
  eigen_assert(m_analysisIsOk && "You must first call analyzePattern()");
  SparseMatrix<Scalar,RowMajor, StorageIndex> mat;
  mat = amat.twistedBy(m_Pinv);
 
  // Initialization
  jr.fill(-1);
  ju.fill(0);
  u.fill(0);
 
  // number of largest elements to keep in each row:
  Index fill_in = (amat.nonZeros()*m_fillfactor)/n + 1;
  if (fill_in > n) fill_in = n;
 
  // number of largest nonzero elements to keep in the L and the U part of the current row:
  Index nnzL = fill_in/2;
  Index nnzU = nnzL;
  m_lu.reserve(n * (nnzL + nnzU + 1));
 
  // global loop over the rows of the sparse matrix
  for (Index ii = 0; ii < n; ii++)
  {
    // 1 - copy the lower and the upper part of the row i of mat in the working vector u
 
    Index sizeu = 1; // number of nonzero elements in the upper part of the current row
    Index sizel = 0; // number of nonzero elements in the lower part of the current row
    ju(ii)    = convert_index<StorageIndex>(ii);
    u(ii)     = 0;
    jr(ii)    = convert_index<StorageIndex>(ii);
    RealScalar rownorm = 0;
 
    typename FactorType::InnerIterator j_it(mat, ii); // Iterate through the current row ii
    for (; j_it; ++j_it)
    {
      Index k = j_it.index();
      if (k < ii)
      {
        // copy the lower part
        ju(sizel) = convert_index<StorageIndex>(k);
        u(sizel) = j_it.value();
        jr(k) = convert_index<StorageIndex>(sizel);
        ++sizel;
      }
      else if (k == ii)
      {
        u(ii) = j_it.value();
      }
      else
      {
        // copy the upper part
        Index jpos = ii + sizeu;
        ju(jpos) = convert_index<StorageIndex>(k);
        u(jpos) = j_it.value();
        jr(k) = convert_index<StorageIndex>(jpos);
        ++sizeu;
      }
      rownorm += numext::abs2(j_it.value());
    }
 
    // 2 - detect possible zero row
    if(rownorm==0)
    {
      m_info = NumericalIssue;
      return;
    }
    // Take the 2-norm of the current row as a relative tolerance
    rownorm = sqrt(rownorm);
 
    // 3 - eliminate the previous nonzero rows
    Index jj = 0;
    Index len = 0;
    while (jj < sizel)
    {
      // In order to eliminate in the correct order,
      // we must select first the smallest column index among  ju(jj:sizel)
      Index k;
      Index minrow = ju.segment(jj,sizel-jj).minCoeff(&k); // k is relative to the segment
      k += jj;
      if (minrow != ju(jj))
      {
        // swap the two locations
        Index j = ju(jj);
        swap(ju(jj), ju(k));
        jr(minrow) = convert_index<StorageIndex>(jj);
        jr(j) = convert_index<StorageIndex>(k);
        swap(u(jj), u(k));
      }
      // Reset this location
      jr(minrow) = -1;
 
      // Start elimination
      typename FactorType::InnerIterator ki_it(m_lu, minrow);
      while (ki_it && ki_it.index() < minrow) ++ki_it;
      eigen_internal_assert(ki_it && ki_it.col()==minrow);
      Scalar fact = u(jj) / ki_it.value();
 
      // drop too small elements
      if(abs(fact) <= m_droptol)
      {
        jj++;
        continue;
      }
 
      // linear combination of the current row ii and the row minrow
      ++ki_it;
      for (; ki_it; ++ki_it)
      {
        Scalar prod = fact * ki_it.value();
        Index j     = ki_it.index();
        Index jpos  = jr(j);
        if (jpos == -1) // fill-in element
        {
          Index newpos;
          if (j >= ii) // dealing with the upper part
          {
            newpos = ii + sizeu;
            sizeu++;
            eigen_internal_assert(sizeu<=n);
          }
          else // dealing with the lower part
          {
            newpos = sizel;
            sizel++;
            eigen_internal_assert(sizel<=ii);
          }
          ju(newpos) = convert_index<StorageIndex>(j);
          u(newpos) = -prod;
          jr(j) = convert_index<StorageIndex>(newpos);
        }
        else
          u(jpos) -= prod;
      }
      // store the pivot element
      u(len)  = fact;
      ju(len) = convert_index<StorageIndex>(minrow);
      ++len;
 
      jj++;
    } // end of the elimination on the row ii
 
    // reset the upper part of the pointer jr to zero
    for(Index k = 0; k <sizeu; k++) jr(ju(ii+k)) = -1;
 
    // 4 - partially sort and insert the elements in the m_lu matrix
 
    // sort the L-part of the row
    sizel = len;
    len = (std::min)(sizel, nnzL);
    typename Vector::SegmentReturnType ul(u.segment(0, sizel));
    typename VectorI::SegmentReturnType jul(ju.segment(0, sizel));
    internal::QuickSplit(ul, jul, len);
 
    // store the largest m_fill elements of the L part
    m_lu.startVec(ii);
    for(Index k = 0; k < len; k++)
      m_lu.insertBackByOuterInnerUnordered(ii,ju(k)) = u(k);
 
    // store the diagonal element
    // apply a shifting rule to avoid zero pivots (we are doing an incomplete factorization)
    if (u(ii) == Scalar(0))
      u(ii) = sqrt(m_droptol) * rownorm;
    m_lu.insertBackByOuterInnerUnordered(ii, ii) = u(ii);
 
    // sort the U-part of the row
    // apply the dropping rule first
    len = 0;
    for(Index k = 1; k < sizeu; k++)
    {
      if(abs(u(ii+k)) > m_droptol * rownorm )
      {
        ++len;
        u(ii + len)  = u(ii + k);
        ju(ii + len) = ju(ii + k);
      }
    }
    sizeu = len + 1; // +1 to take into account the diagonal element
    len = (std::min)(sizeu, nnzU);
    typename Vector::SegmentReturnType uu(u.segment(ii+1, sizeu-1));
    typename VectorI::SegmentReturnType juu(ju.segment(ii+1, sizeu-1));
    internal::QuickSplit(uu, juu, len);
 
    // store the largest elements of the U part
    for(Index k = ii + 1; k < ii + len; k++)
      m_lu.insertBackByOuterInnerUnordered(ii,ju(k)) = u(k);
  }
  m_lu.finalize();
  m_lu.makeCompressed();
 
  m_factorizationIsOk = true;
  m_info = Success;
}

info()

template<typename Scalar_ , typename StorageIndex_ = int>

ComputationInfo Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::info ( ) const

inline

Reports whether previous computation was successful.

Returns

Success if computation was successful, NumericalIssue if the matrix.appears to be negative.

Definition at line 144 of file IncompleteLUT.h.

    {
      eigen_assert(m_isInitialized && "IncompleteLUT is not initialized.");
      return m_info;
    }

rows()

template<typename Scalar_ , typename StorageIndex_ = int>

EIGEN_CONSTEXPR Index Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::rows ( void  ) const

inline

Definition at line 135 of file IncompleteLUT.h.

{ return m_lu.rows(); }

setDroptol()

template<typename Scalar , typename StorageIndex >

void Eigen::IncompleteLUT< Scalar, StorageIndex >::setDroptol

(

const RealScalar &

droptol

)

Set control parameter droptol

Parameters

droptol

Drop any element whose magnitude is less than this tolerance

Definition at line 208 of file IncompleteLUT.h.

{
  this->m_droptol = droptol;
}

setFillfactor()

template<typename Scalar , typename StorageIndex >

void Eigen::IncompleteLUT< Scalar, StorageIndex >::setFillfactor

(

int

fillfactor

)

Set control parameter fillfactor

Parameters

fillfactor

This is used to compute the number fill_in of largest elements to keep on each row.

Definition at line 218 of file IncompleteLUT.h.

{
  this->m_fillfactor = fillfactor;
}

Member Data Documentation

m_analysisIsOk

template<typename Scalar_ , typename StorageIndex_ = int>

bool Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_analysisIsOk

protected

Definition at line 196 of file IncompleteLUT.h.

m_droptol

template<typename Scalar_ , typename StorageIndex_ = int>

RealScalar Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_droptol

protected

Definition at line 194 of file IncompleteLUT.h.

m_factorizationIsOk

template<typename Scalar_ , typename StorageIndex_ = int>

bool Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_factorizationIsOk

protected

Definition at line 197 of file IncompleteLUT.h.

m_fillfactor

template<typename Scalar_ , typename StorageIndex_ = int>

int Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_fillfactor

protected

Definition at line 195 of file IncompleteLUT.h.

m_info

template<typename Scalar_ , typename StorageIndex_ = int>

ComputationInfo Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_info

protected

Definition at line 198 of file IncompleteLUT.h.

m_isInitialized

template<typename Scalar_ , typename StorageIndex_ = int>

bool Eigen::SparseSolverBase< Derived >::m_isInitialized

mutableprotected

Definition at line 123 of file SparseSolverBase.h.

m_lu

template<typename Scalar_ , typename StorageIndex_ = int>

FactorType Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_lu

protected

Definition at line 193 of file IncompleteLUT.h.

m_P

template<typename Scalar_ , typename StorageIndex_ = int>

PermutationMatrix<Dynamic,Dynamic,StorageIndex> Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_P

protected

Definition at line 199 of file IncompleteLUT.h.

m_Pinv

template<typename Scalar_ , typename StorageIndex_ = int>

PermutationMatrix<Dynamic,Dynamic,StorageIndex> Eigen::IncompleteLUT< Scalar_, StorageIndex_ >::m_Pinv

protected

Definition at line 200 of file IncompleteLUT.h.

---

The documentation for this class was generated from the following file:

• IncompleteLUT.h