Eigen::KroneckerProductSparse< Lhs, Rhs > Class Template Reference

Kronecker tensor product helper class for sparse matrices. More...

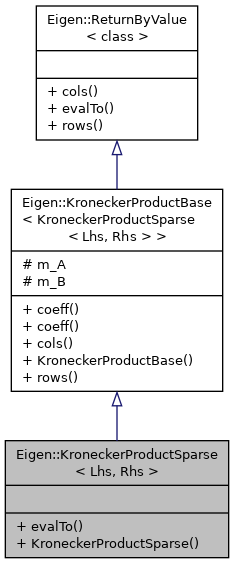
Inheritance diagram for Eigen::KroneckerProductSparse< Lhs, Rhs >:

Public Member Functions
template<typename Dest >
void	evalTo (Dest &dst) const
	Evaluate the Kronecker tensor product. More...
	KroneckerProductSparse (const Lhs &A, const Rhs &B)
	Constructor. More...
Public Member Functions inherited from Eigen::KroneckerProductBase< KroneckerProductSparse< Lhs, Rhs > >
Scalar	coeff (Index i) const
Scalar	coeff (Index row, Index col) const
Index	cols () const
	KroneckerProductBase (const Lhs &A, const Rhs &B)
	Constructor. More...
Index	rows () const
Public Member Functions inherited from Eigen::ReturnByValue< class >
EIGEN_CONSTEXPR Index	cols () const EIGEN_NOEXCEPT
void	evalTo (Dest &dst) const
EIGEN_CONSTEXPR Index	rows () const EIGEN_NOEXCEPT

Private Types
typedef KroneckerProductBase< KroneckerProductSparse >	Base

Additional Inherited Members
Public Types inherited from Eigen::ReturnByValue< class >
typedef internal::dense_xpr_base< ReturnByValue >::type	Base
typedef internal::traits< Derived >::ReturnType	ReturnType
Protected Types inherited from Eigen::KroneckerProductBase< KroneckerProductSparse< Lhs, Rhs > >
typedef Traits::Lhs	Lhs
typedef Traits::Rhs	Rhs
Protected Attributes inherited from Eigen::KroneckerProductBase< KroneckerProductSparse< Lhs, Rhs > >
Lhs::Nested	m_A
Rhs::Nested	m_B

Detailed Description

template<typename Lhs, typename Rhs>
class Eigen::KroneckerProductSparse< Lhs, Rhs >

Kronecker tensor product helper class for sparse matrices.

If at least one of the operands is a sparse matrix expression, then this class is returned and evaluates into a sparse matrix.

This class is the return value of kroneckerProduct(EigenBase, EigenBase). Use the function rather than construct this class directly to avoid specifying template prarameters.

Template Parameters

Lhs	Type of the left-hand side, a matrix expression.
Rhs	Type of the rignt-hand side, a matrix expression.

Definition at line 117 of file KroneckerTensorProduct.h.

Member Typedef Documentation

Base

template<typename Lhs , typename Rhs >

typedef KroneckerProductBase<KroneckerProductSparse> Eigen::KroneckerProductSparse< Lhs, Rhs >::Base

private

Definition at line 120 of file KroneckerTensorProduct.h.

Constructor & Destructor Documentation

KroneckerProductSparse()

template<typename Lhs , typename Rhs >

Eigen::KroneckerProductSparse< Lhs, Rhs >::KroneckerProductSparse ( const Lhs &  A, const Rhs &  B  )

inline

Constructor.

Definition at line 126 of file KroneckerTensorProduct.h.

      : Base(A, B)
    {}

Member Function Documentation

evalTo()

template<typename Lhs , typename Rhs >

template<typename Dest >

void Eigen::KroneckerProductSparse< Lhs, Rhs >::evalTo

(

Dest &

dst

)

const

Evaluate the Kronecker tensor product.

Definition at line 149 of file KroneckerTensorProduct.h.

{
  Index Br = m_B.rows(), Bc = m_B.cols();
  dst.resize(this->rows(), this->cols());
  dst.resizeNonZeros(0);
  
  // 1 - evaluate the operands if needed:
  typedef typename internal::nested_eval<Lhs,Dynamic>::type Lhs1;
  typedef internal::remove_all_t<Lhs1> Lhs1Cleaned;
  const Lhs1 lhs1(m_A);
  typedef typename internal::nested_eval<Rhs,Dynamic>::type Rhs1;
  typedef internal::remove_all_t<Rhs1> Rhs1Cleaned;
  const Rhs1 rhs1(m_B);
    
  // 2 - construct respective iterators
  typedef Eigen::InnerIterator<Lhs1Cleaned> LhsInnerIterator;
  typedef Eigen::InnerIterator<Rhs1Cleaned> RhsInnerIterator;
  
  // compute number of non-zeros per innervectors of dst
  {
    // TODO VectorXi is not necessarily big enough!
    VectorXi nnzA = VectorXi::Zero(Dest::IsRowMajor ? m_A.rows() : m_A.cols());
    for (Index kA=0; kA < m_A.outerSize(); ++kA)
      for (LhsInnerIterator itA(lhs1,kA); itA; ++itA)
        nnzA(Dest::IsRowMajor ? itA.row() : itA.col())++;
      
    VectorXi nnzB = VectorXi::Zero(Dest::IsRowMajor ? m_B.rows() : m_B.cols());
    for (Index kB=0; kB < m_B.outerSize(); ++kB)
      for (RhsInnerIterator itB(rhs1,kB); itB; ++itB)
        nnzB(Dest::IsRowMajor ? itB.row() : itB.col())++;
    
    Matrix<int,Dynamic,Dynamic,ColMajor> nnzAB = nnzB * nnzA.transpose();
    dst.reserve(VectorXi::Map(nnzAB.data(), nnzAB.size()));
  }
 
  for (Index kA=0; kA < m_A.outerSize(); ++kA)
  {
    for (Index kB=0; kB < m_B.outerSize(); ++kB)
    {
      for (LhsInnerIterator itA(lhs1,kA); itA; ++itA)
      {
        for (RhsInnerIterator itB(rhs1,kB); itB; ++itB)
        {
          Index i = itA.row() * Br + itB.row(),
                j = itA.col() * Bc + itB.col();
          dst.insert(i,j) = itA.value() * itB.value();
        }
      }
    }
  }
}

---

The documentation for this class was generated from the following file:

• KroneckerTensorProduct.h