Iterative Solvers module
Classes | |
| class | Eigen::DGMRES< MatrixType_, Preconditioner_ > |
| A Restarted GMRES with deflation. This class implements a modification of the GMRES solver for sparse linear systems. The basis is built with modified Gram-Schmidt. At each restart, a few approximated eigenvectors corresponding to the smallest eigenvalues are used to build a preconditioner for the next cycle. This preconditioner for deflation can be combined with any other preconditioner, the IncompleteLUT for instance. The preconditioner is applied at right of the matrix and the combination is multiplicative. More... | |
| class | Eigen::GMRES< MatrixType_, Preconditioner_ > |
| A GMRES solver for sparse square problems. More... | |
| class | Eigen::IDRS< MatrixType_, Preconditioner_ > |
| The Induced Dimension Reduction method (IDR(s)) is a short-recurrences Krylov method for sparse square problems. More... | |
| class | Eigen::IDRSTABL< MatrixType_, Preconditioner_ > |
| The IDR(s)STAB(l) is a combination of IDR(s) and BiCGSTAB(l). It is a short-recurrences Krylov method for sparse square problems. It can outperform both IDR(s) and BiCGSTAB(l). IDR(s)STAB(l) generally closely follows the optimal GMRES convergence in terms of the number of Matrix-Vector products. However, without the increasing cost per iteration of GMRES. IDR(s)STAB(l) is suitable for both indefinite systems and systems with complex eigenvalues. More... | |
| class | Eigen::MINRES< MatrixType_, UpLo_, Preconditioner_ > |
| A minimal residual solver for sparse symmetric problems. More... | |
Detailed Description
This module aims to provide various iterative linear and non linear solver algorithms. It currently provides:
- a Householder GMRES implementation
- an IDR(s) implementation
- a BiCGSTAB(L) implementation
- a DGMRES implementation
- a MINRES implementation
- a IDRSTABL implementation
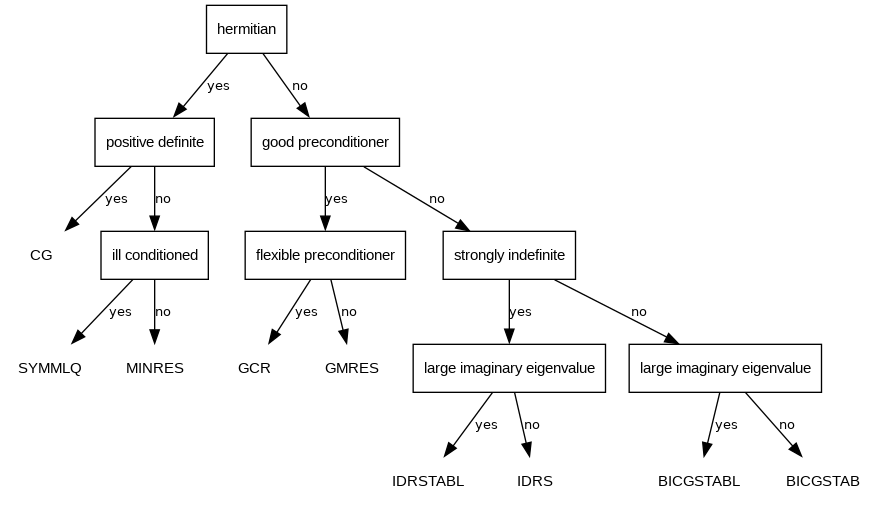
Choosing the best solver for solving A x = b depends a lot on the preconditioner chosen as well as the properties of A. The following flowchart might help you.